Persamaan Garis yang melalui dua titik

3. Persamaan garis yang melalui dua titik

Gradien garis yang melalui titik (x₁, y₁) dan (x₂, y₂) yaitu seperti pada gambar di bawah ini,

Selanjutnya dengan menggunakan rumus persamaan garis dengan gradient m dan melalui sebuah titik (x₁ , y₁), yaitu y - y₁ = m ( x - x₁ ) dapat diperoleh rumus berikut :

y - y₁ = m ( x - x₁ )

y - y₁

y - y₁ = y₂ - y₁

Kesimpulan :

Persamaan garis yang melalui titik (x₁, y₁) dan (x₂, y₂) yaitu :

Contoh 1

Perhatikan gambar di bawah ini !

Tentukanlah persamaan garis l !

 

Penyelesaian :

Garis l melalui titik A(3,4) dan titik B(5,8).

P(3,4) berarti x₁ = 3 , y₁ = 4

Q(5,8) berarti x₂ = 5 , y₂ = 8

Persamaan garis l yang melalui titik A(3,4) dan titik B(5,8) adalah :

2(y - 4) = 4(x - 3)

2y - 8 = 4x - 12

2y - 4x = 8 - 12

2y - 4x = -4

y - 2x = -2

Jadi persamaan garis l yang melalui titik A(3,4) dan titik B(5,8) adalah y - 2x = -2.

Nilai Optimum Suatu Fungsi Objektif

Seperti yang telah kita ketahui bersama, suatu permasalahan dapat dituliskan dalam bahasa matematika. Suatu permasalahan tentu mempunyai bentuk penyelesaian yang optimum.

1. Fungsi Objektif z = ax + by

Fungsi tujuan dalam pembuatan model matematika dinyatakan dalam bentuk z = ax + by. Bentuk z = ax + by yang akan dioptimumkan (dimaksimumkan atau diminimumkan) tersebut disebut juga fungsi objektif. Jadi, fungsi objektif dari program linear adalah fungsi z = ax + by yang akan ditentukan nilai optimumnya. Misalnya sebagai berikut.

a. Fungsi objektif: memaksimumkan z = x + y

Kendala: 5x + 4y ≤ 20

x + 2y ≤ 24

x, y ≥ 0, dengan x, y ϵ C

b. Fungsi objektif: meminimumkan z = 2x + 3y

Kendala: x + y ≤ 500

4x + 2y ≤ 200

x, y ≥ 0

x, y ϵ C

2. Cara Menentukan Nilai Optimum Fungsi Objektif

Dari uraian yang telah diberikan, kita dapat mengetahui tujuan utama dari program linear, yaitu menentukan nilai optimum (maksimum/minimum) dari suatu fungsi objektif. Untuk menyelesaikan masalah program linear yang berhubungan dengan nilai optimum, langkah-langkah pemecahannya adalah sebagai berikut.

a. Merumuskan permasalahan ke dalam model matematika.

b. Membentuk sistem pertidaksamaan linear yang sesuai.

c. Menggambarkan kendala sebagai daerah di bidang Cartesius yang memenuhi sistem pertidaksamaan linear.

d. Menentukan nilai optimum (maksimum/minimum) dari fungsi objektif.

e. Menafsirkan/menjawab permasalahan.

Untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode garis selidik, lakukanlah langkah-langkah berikut: Tentukan model pertidaksamaan dari informasi soal dan gambarkan daerah selesaian dari sistem pertidaksamaan tersebut pada bidang koordinat. Tentukan garis selidik ax + by = k apabila fungsi objektifnya f(x, y) = ax + by, a, b, dan k bilangan real. Untuk menentukan nilai maksimum fungsi objektif maka carilah garis selidik dengan nilai k terbesar dan melalui titik (-titik) pada daerah selesaian. Sedangkan untuk menentukan nilai minimum fungsi objektif maka carilah garis selidik dengan nilai k terkecil dan melalui titik (-titik) pada daerah selesaian. Untuk lebih memahami penerapan langkah-langkah tersebut, perhatikan contoh soal berikut. Contoh Soal Seorang peternak ayam petelur harus memberi makanan untuk tiap 50 ekor/hari paling sedikit 150 unit zat A dan 200 unit zat B. Zat-zat tersebut tidak dapat dibeli dalam bentuk murni, melainkan teerdapat dalam makanan ayam M1 dan M2. Tiap kg makanan ayam M1 mengandung 30 unit zat A dan 20 unit zat B, dan makanan M2 mengandung 20 unit zat A dan 40 unit zat B. Jika harga M1 adalah Rp 225/kg dan harga M2 adalah Rp 250/kg, dan tiap ekor membutuhkan 125 gr makanan/hari. Berapakah banyaknya makanan M1 dan M2 harus dibeli tiap hari untuk 1000 ekor ayam petelur, supaya harganya semurah-murahnya dan kebutuhan akan zat-zat itu dipenuhi? Ayam Pembahasan Contoh Soal Langkah pertama: Ubah permasalahan di atas menjadi model matematika. Misalkan x dan y secara berturut adalah banyaknya makanan M1 dan M2 yang harus dibeli tiap hari untuk 1000 ekor ayam petelur. Karena tiap 50 ekor ayam dalam tiap harinya harus makan paling sedikit 150 unit zat A dan 200 unit zat B, tiap 1.000 ekor ayam dalam tiap harinya harus makan paling sedikit 3.000 unit zat A dan 4.000 unit zat B maka. Dan karena tiap ekor membutuhkan 125 gr makanan/hari, maka 1.000 ekor ayam membutuhkan 125.000 gr atau 125 kg makanan tiap harinya. Sehingga permasalahan di atas dapat dimodelkan sebagai berikut. 30x + 20y ≥ 3.000 20x + 40y ≥ 4.000 x + y ≥ 125 x ≥ 0 y≥ 0 x, y bilangan cacah Fungsi objektif dari permasalahan di atas adalah f(x, y) = 225x + 250y. Sebelum menggambar grafiknya, sebaiknya kita daftar titik-titik yang dilalui oleh garis-garis batas dari sistem pertidaksamaan di atas. Tabel Titik-titik Koordinat Apabila digambarkan, daerah selesaiannya seperti berikut. Daerah Selesaian Langkah kedua: Gambarkan garis selidik 225x + 250y = k. Garis-garis Selidik Setelah melihat gambar di atas, ternyata garis selidik yang melalui titik (50, 75) yang memiliki nilai k minimum (nilai k bisa dilihat pada sumbu y, semakin tinggi titik potong garis selidik terhadap sumbu y, maka semakin besar pula nilai k tersebut, dan sebaliknya). Untuk x = 50 dan y = 75, diperoleh nilai k-nya adalah 30.000. Jadi, banyaknya makanan M1 dan M2 harus dibeli tiap hari untuk 1000 ekor ayam petelur supaya harganya semurah-murahnya dan kebutuhan akan zat-zat itu dipenuhi secara berturut-turut adalah 50 kg dan 75 kg.

Make Money at : http://bit.ly/copy_win

Persamaan Garis Lurus

A. Pengertian Persamaan Garis Lurus

Sebelum memahami pengertian persamaan garis lurus, ada baiknya kamu mengingat kembali materi tentang koordinat Cartesius persamaan garis lurus selalu digambarkan dalam koordinat Cartesius. Untuk itu, pelajarilah uraian berikut.

1. Koordinat Cartesius

Dalam sebuah bidang,terdapat dua garis yaitu mendatar (horizontal) dan tegak (vertikal), kedua garis tersebut berpotongan tegak lurus pada titik nol. Dua garis itu disebut sumbu koordinat . Sumbu mendatar (sumbu x) , sumbu tegak (sumbu y). Titik potong kedua sumbu di sebut titik pusat koordinat . Jika disatukan dalam sebuah bidang, maka itulah yng disebut bidang koordinat cartesius.

B. Gradien

perbandingan ordinat dan absis ini disebut sebagai gradien.
Biasanya gradien dilambangkan dengan m.
Jadi, Gradien adalah tingkat kemiringan garis.
Dari uraian tersebut diperoleh rumus umum untuk mencari gradien pada garis yang melalui dua titik, sebagai berikut.

Sifat-Sifat Persamaan Garis

a. Garis yang Sejajar dengan Sumbu-x

.Jika garis sejajar dengan sumbu x maka  nilai gradiennya adalah nol

b. Gradien garis yang sejajar dengan sumbu-y

Gradien garis yang sejajar dengan sumbu y bentuknya sama dengan sumbu x, gambarnya menyerupai gradien garis sejajar dengan sumbu x yang membedakan ialah arah sejajarnya. Jika sejajar dengan sumbu x maka arahnya vertikal sedangkan jika sejajar dengan sumbu y maka arahnya horizontal.

Jika garis sejajar dengan sumbu-y maka garis tersebut tidak memiliki gradien.

c. Gradien Dua Garis yang Sejajar
Sekarang coba kamu perhatikan Gambar 3.6

Garis k dan l merupakan dua garis yang sejajar. Bagaimana gradien kedua garis tersebut? Perhatikan uraian berikut.
• Garis k melalui titik A(–2, 0) dan B(0, 2).
Untuk titik A(–2, 0) maka x₁ = –2, y₁ = 0.
Untuk titik B(0, 2) maka x₂ = 0, y₂ = 2.

Mab = y₂ – y₁ = 2 – 0 = 2

       ______________   = 1

        X_{2 –} x₁ = 0 –(-2) = 2

• Garis l melalui titik C(0, –1) dan D(1, 0).
Untuk titik C(0, –1) maka x₁ = 0, y₁ = –1.
Untuk titik D(1, 0) maka x₂ = 1, y₂ = 0.

Mcd = y_{2 –} y₁  = 0 –(-1) = 1

        _______________   = 1

         X₂ – x₁ = 1 - 0 = 1

Dari uraian tersebut terlihat bahwa garis k dan l memiliki gradien yang sama.

Setiap garis yang sejajar memiliki gradien yang sama.

d. Gradien Dua Garis yang Tegak Lurus

• Garis k melalui titik C(3, 0) dan D(0, 3).
Untuk titik C(3, 0) maka x₁ = 3, y₁ = 0.
Untuk titik D(0, 3) maka x₂ = 0, y₂ = 3.

Mcd = y₂ – y₁ = 3 – 0 = 3

       ______________   = -1

        X_{2 –} x₁ = 0 – 3 = -3

• Garis l melalui titik A(–1, 0) dan B(0, 1).
Untuk titik A(–1, 0) maka x₁ = –1, y₁ = 0.
Untuk titik B(0, 1) maka x₂ = 0, y₂ = 1.

Mab = y_{2 –} y₁  = 1 – 0 = 1

        _______________   = 1

         X₂ – x₁ = 0 – (-1) = 1

Hasil kali kedua gradien tersebut adalah

m_AB × m_CD = 1 × –1 = –1
Uraian tersebut memperjelas hal berikut:

Hasil kali antara dua gradien dari garis yang saling tegak lurus adalah –1.

C. Menentukan Persamaan Garis Lurus

Bentuk y = mx merupakan bentuk persamaan garis lurus sederhana. Dikatakan sebagai bentuk sederhana karena garis yang dibentuk oleh persamaan garis tersebut selalu melalui titik pusat koordinat. Untuk lebih jelasnya, perhatikan Contoh Soal

Contoh Soal :Tentukan persamaan garis untuk garis yang melalui titik O (0, 0) dan memiliki: a. gradien 2, b. gradien –3, c. gradien 1. Jawab :  y = 2xÞa. y = mx maka y = (2)x  y = –3xÞb. y = mx maka y = (–3)x  y = xÞc. y = mx maka y = (1)x

Adapun bentuk umum dari persamaan garis lurus dapat dituliskan sebagai berikut.

Persamaan garis ini hampir sama dengan bentuk sederhananya, namun diberi tambahan konstanta (diberi lambang c). Hal ini menunjukkan bahwa garis yang dibentuk oleh persamaan garis tersebut tidak akan melalui titik O(0, 0).
Setelah kamu memahami bentuk sederhana dan bentuk umum persamaan garis, berikut ini akan diuraikan bagaimana menentukan sebuah persamaan garis dari titik koordinat atau gradien.

1. Menentukan Persamaan Garis dari Gradien dan Titik Koordinat

Sekarang, coba kamu perhatikan Gambar 3.1. Gambar tersebut menunjukkan sebuah garis k pada bidang koordinat Cartesius. Garis tersebut melalui titik A(x₁, y₁) dan tidak melalui titik pusat koordinat sehingga persamaan garis pada Gambar 3.8 dapat dituliskan:
y₁ = mx₁ + c ….(1)
Adapun bentuk umum persamaan garis yang tidak melalui titik pusat koordinat dituliskan:
y = mx + c ….(2)

Jika ditentukan selisih dari persamaan (2) dan persamaan (1) maka diperoleh:

Selanjutnya diperoleh rumus umum untuk menentukan persamaan garis jika diketahui gradien dan titik koordinat, yaitu:

2. Menentukan Persamaan Garis yang Melalui Dua Titik

Pada bagian sebelumnya, kamu telah mempelajari cara menentukan persamaan garis yang melalui satu titik koordinat dan gradiennya diketahui. Sekarang, kamu akan mempelajari bagaimana menentukan persamaan garis yang melalui dua titik. Caranya hampir sama dengan rumus umum yang telah dipelajari sebelumnya.
Coba kamu perhatikan uraian berikut :
• y – y1 = m (x – x1) adalah rumus umum persamaan garis dari gradien dan titik koordinat.

Jadi, rumus untuk menentukan persamaan garis yang melalui dua titik koordinat adalah

3. Menentukan Koordinat Titik Potong dari Dua Garis Lurus

Coba kamu perhatikan Gambar 3.12

Dari Gambar 3.9 , terdapat dua garis dalam bidang koordinat, yaitu garis k dan l. Dalam Gambar 3.9(a) , kedua garis tersebut sejajar. Adapun pada Gambar 3.9(b) , kedua garis tersebut tidak sejajar sehingga keduanya berpotongan di suatu titik, yaitu titik A (x1, y1). Jadi, koordinat titik potong dapat dicari dari dua garis yang tidak sejajar.
Sekarang, bagaimana cara menentukan koordinat titik potong dari dua persamaan garis yang diketahui? Ada dua cara yang dapat digunakan, yaitu cara menggambar (cara grafik) dan cara substitusi. Untuk itu, pelajari uraian berikut.
a. Cara Grafik
Dengan cara ini, dua persamaan garis digambar ke dalam bidang koordinat Cartesius sehingga koordinat titik potong kedua garis tersebut dapat dilihat dari gambar.

b. Cara Substitusi
Dengan cara substitusi, salah satu variabel dari persamaan garis yang diketahui dimasukkan (disubstitusikan) ke dalam variabel yang sama dari persamaan garis yang lain.

Contoh :

2x - 3y = 2 . 2

4x - 10y= -8 -

4x - 6y = 4

4x - 10y= -8 -

4y = 4

 y = 1

4. Aplikasi Persaman Garis Lurus

Dalam kehidupan sehari-hari, banyak sekali bidang-bidang yang menggunakan aplikasi persamaan garis lurus. Misalnya, perhitungan kecepatan-jarak-waktu dalam fisika dan perhitungan harga barang dan titik impas dalam ekonomi. Coba kamu pelajari Contoh Soal. Aplikasi Persaman Garis Lurus Dalam kehidupan sehari-hari, banyak sekali bidang-bidang yang menggunakan aplikasi persamaan garis lurus. Misalnya, perhitungan kecepatan-jarak-waktu dalam fisika dan perhitungan harga barang dan titik impas dalam ekonomi.

Sistem Persamaan Linier Dua Variabel

Pengertian Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem persamaan linear dua variabel, atau sering disingkat sebagai SPLDV, seringkali digunakan untuk memecahkan permasalahan di sekitar kita. Sebelum kita mempelajari SPLDV, sebaiknya kita kenal dulu persamaan linear dua variabel. Perhatikan permasalahan berikut.

Anggita akan berencana membeli pensil dan bolpoin di suatu toko alat tulis. Ia berencana akan membeli total sebanyak 5 buah alat tulis. Berapa banyaknya masing-masing pensil dan bolpoin yang mungkin dibeli oleh Anggita?

Untuk mendaftar semua kemungkinannya, kita dapat menggunakan tabel seperti berikut.

Permasalahan di atas dapat dituliskan dalam bentuk persamaan sebagai berikut.

dengan p dan b secara berturut-turut merupakan banyaknya pensil dan bolpoin yang akan dibeli oleh Anggita.
Karena banyakanya pensil ditambah banyaknya bolpoin adalah 5 buah, maka banyaknya pensil sama dengan 5 dikurangi banyaknya bolpoin dan demikian juga banyaknya bolpoin sama dengan 5 dikurangi dengan banyaknya pensil. Atau dengan kata lain, persamaan p + b = 5 dapat juga dituliskan menjadi bentuk persamaan berikut.

Berikut ini beberapa contoh bentuk persamaan linear dua variabel lannya.

Sistem Persamaan Linear Dua Variabel (SPLDV)
Setelah mengenal persamaan linear dua variabel, selanjutnya kita lanjutkan pembahasan kita ke SPLDV. Perhatikan permasalahan berikut.

Pergi ke Kantin
Pada saat jam istirahat sekolah, Ana dan Andika bersama-sama pergi ke kantin sekolah. Ana membeli 3 buah pisang goreng dan 2 donat dengan harga seluruhnya Rp 3.500,00. Sedangkan Andika membeli 4 buah pisang goreng dan 2 donat dengan harga seluruhnya Rp 4.000,00. Berapakah harga masing-masing pisang goreng dan donat per buahnya?

Misalkan x dan y secara berturut-turut merupakan harga satuan pisang goreng dan donat yang telah dibeli di kantin sekolah tersebut. Karena Ana membeli 3 pisang goreng dan 2 donat dengan harga seluruhnya Rp 3.500,00, maka kalimat tersebut dapat dimodelkan ke dalam persamaan,

Sedangkan Andika membeli 4 buah pisang goreng dan 2 donat dengan harga seluruhnya Rp 4.000,00, maka kalimat tersebut dapat dituliskan ke dalam persamaan,

Persamaan-persamaan 3x + 2x = 3.500 dan 4x + 2y = 4.000 merupakan persamaan-persamaan yang berhubungan, karena kedua persamaan tersebut memiliki 2 variabel yang sama. Mudahnya, kedua persamaan tersebut dimodelkan dari transaksi Ana dan Andika ketika mereka berdua membeli dua makanan yang sama di kantin yang juga sama. Sehingga, transaksi yang dilakukan oleh Ana akan sesuai dengan transaksi yang dilakukan oleh Andika. Artinya, transaksi mereka berdua dipengaruhi oleh harga satuan pisang goreng dan donat pada kantin tersebut. Sehingga, kedua persamaan 3x + 2x = 3.500 dan 4x + 2y = 4.000 disebut sebagai suatu sistem. Karena sistem tersebut terdiri dari persamaan-persamaan linear dua variabel, maka sistem tersebut disebut sistem persamaan linear dua variabel.
Sistem persamaan linear dua variabel tersebut dapat dituliskan sebagai berikut.

Selanjutnya, dapatkah kita menentukan harga masing-masing pisang goreng dan donat yang telah dibeli oleh Ana dan Andika? Perhatikan bahwa banyaknya donat yang mereka beli adalah sama, yaitu 2 buah. Sedangkan banyaknya pisang goreng yang dibeli oleh Ana lebih sedikit 1 buah daripada yang dibeli oleh Andika. Karena Andika mengeluarkan uang Rp 4.000,00 untuk membeli semua makanan ringannya, sedangkan Ana mengeluarkan Rp 500,00 lebih sedikit daripada Andika, maka dengan mudah kita dapat menyimpulkan bahwa harga pisang gorengnya adalah Rp 500,00 tiap buahnya.
Apabila harga pisang goreng tiap buahnya adalah Rp 500,00, maka selanjutnya kita dapat menentukan harga 1 buah donat dengan menggunakan transaksi Ana atau Andika. Kali ini kita akan menggunakan transaksi Ana untuk menentukan harga 1 donat.

Sehingga diperoleh harga satu donat adalah Rp 1.000,00. Apakah jawaban ini benar? Untuk mengetahui kebenarannya, kita dapat mengujinya ke dalam permasalahan.
Ana membeli 3 pisang goreng dan 2 donat, maka dia harus membayar 3 × 500 + 2 × 1.000 = 1.500 + 2.000 = 3.500. Untuk kasus Ana, harga pisang goreng dan donat memenuhi. Selanjutnya kita uji juga ke dalam kasusnya Andika. Andika membeli 4 pisang goreng dan 2 donat, maka dia harus membayar 4 × 500 + 2 × 1.000 = 2.000 + 2.000 = 4.000. Harga satuan pisang goreng dan donat yang telah kita cari ternyata memenuhi kedua persamaan yang diberikan. Sehingga dapat dikatakan bahwa x = 500 dan y = 1.000 merupakan selesaian dari SPLDV tersebut.
Catatan Selesaian dari SPLDV merupakan nilai dua variabel yang memenuhi kedua persamaan yang terdapat dalam SPLDV tersebut. Apabila nilai dua variabel tersebut hanya memenuhi salah satu persamaan saja, atau bahkan tidak memenuhi keduanya, maka nilai variabel-variabel tersebut bukanlah selesaian dari SPLDV tersebut.
Sebagai ilustrasi, x = 1.000 dan y = 250 memenuhi persamaan 3x + 2y = 3.500. Akan tetapi nilai tersebut tidak memenuhi persamaan kedua karena 4 × 1.000 + 2 × 250 = 4.500 ≠ 4.000. Sehingga x = 1.000 dan y = 250 bukan selesaian dari SPLDV yang terdiri dari persamaan-persamaan 3x + 2y = 3.500 dan 4x + 2y = 3.500. Semoga bermanfaat, yos3prens.

Trigonometri

Trigonometri 

Trigonometri : merupakan cabang ilmu matematika yang mempelajari tentang garis dan sudut suatu segitiga.
Hubungan antara garis dan sudut ini lah yang akan menjadi fungsi-fungsi trigonometri.
Berikut ini adalah fungsi dasarnya (sinus, cosinus, tangen):
Pada segitiga ABC di samping, dengan panjang AB adalah q, BC = p, dan AC = r, serta sudut CAB = X, maka berlaku:
, ,
Kemudian , ,

Trigonometri Untuk Sudut Istimewa

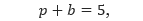
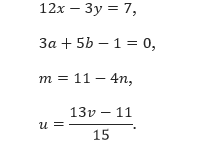
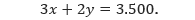
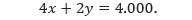
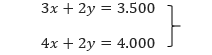
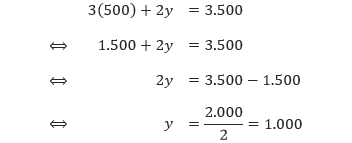
Pada sudut istimewa, yaitu dan kelipatannya, nilai sinus, cosinus, dan tangennya berupa bilangan sederhana, seperti pada tabel di samping.
Sedangkan nilai sec, cosec, dan cot dapat diperoleh dengan menggunakan hubungannya dengan sin, cos, dan tan di atas.
Nilai sin, cos, dan tan sudut istimewa ini harus hafal, karena akan selalu digunakan untuk materi lainnya seperti integral, limit, dll.
Contoh soal:
Pada segitiga siku-siku ABC dengan sisi miring BC dan sisi tegak AB, panjang BC = 5cm, dan panjang AB = 4cm, tentukanlah nilai dari cos C.
Jawaban:
Cos C = AC/BC. Panjang AB dan BC sudah diketahui, tetapi panjang AC belum harus kita cari terlebih dahulu.
Karena segitiga tersebut siku-siku, maka dapat digunakan dalil pythagoras, yaitu AC^2 = BC^2 – AB^2 =  5^2 – 4^2 = 9. Jadi panjang AC = 3cm
Oleh karena itu,